3√2 133 2√3 18 Categories Mathematics Leave a Reply Cancel reply Your email address will not be published Required fields are marked * Comment Name *Factorise 2√3x2 X 5√3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions Concept Notes & Videos & Videos & Videos 291 Syllabus Advertisement Remove all ads Factorise 2√3x2 X 5√3 MathematicsSelect two answers Amultiply by 4 on both sides Bmultiply by 2x on both sides Csubtract 1/4x from both sides Dadd 1/2 to both sides plz Math How do I solve this problem?

Rd Sharma Class 9th Solutions Chapter 3 Rationalisation
2 root 3 - 5 root 2 and root 3 + 2 root 2
2 root 3 - 5 root 2 and root 3 + 2 root 2-Rationalise the Denominators of 2√5 3√2/2√5 3√2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions Concept Notes & Videos 306 Syllabus Advertisement Remove all ads Rationalise the Denominators of 2√5 3√2/2√5 3√2 Mathematics sec x = 3 > cosx = 1/3 sinx = 2√2/3 , in II the sine is , and I used Pythagoras tan x/2= sinx/2 / cos x/2 Now look how I answered your second question in




How To Solve 1 1 2 2 3 Quora
√5 constructing with ruler and compass the segments of the respective length Explain the construction and argue your solution Categories Mathematics Leave a Reply Cancel reply1) Find all real solutions √x2 √x3=5 What is the solution set? Which could be a first step in solving the equation 1/4x1/2=3/4x in an efficient way?
The question can be solved in the way mentioned below √x y = 7 x √y = 11 In order to simplify the question, we will be taking down the equation into smaller form(Just forTrigonometry Trigonometry questions and answers Evaluate sin (5) OA) 1 OB) 3 2 O OC C) 1 2 OD √2 2 Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33
Rationalise the denominator in each of the following and hence evaluate by taking √2 = 1414, √3 = 1732 and √5 = 2236 up to three places of decimalSOLUTION Given, N = {√(√5 2) √(√5 2)}/√(√5 1) √3 – 2√2 Now, {√√5 2 √√5 – 2}/√√5 1 = { √√5 2 √√5 the sum of the angles MOP and PON is equal to write the set roster formA= {xx is an integer and 2



1




How To Add And Subtract Square Roots 9 Steps With Pictures
Find stepbystep Calculus solutions and your answer to the following textbook question Find the arc length from (0, 3) clockwise to (2, √5) along the circle x²y²=9NCERT Solutions Class 9 Maths Chapter 1 Exercise 15 Question 2 Summary Thus, the simplified values of (3 √3) (2 √2), (3 √3) (3 √3), (√5 √2)², and (√5 √2) (√5 √2) are 6 3√2 2√3 √6, 6, 7 2√10 and 3 respectively a = 2, b = 5, c = 10 ∴ b 2 – 4ac = (5)2 4 × 2 × 10 = 25 – 80 ∴ b 2 – 4ac = 55 iii √2 x 2 4x 2√2 = 0 Comparing the above equation with ax bx c = 0, we get a = √2,b = 4, c = 2√2 ∴ b 2 – 4ac = (4)2 – 4 × √2 × 2√2 = 16 – 16 ∴ b 2 – 4ac =0 Question 3 Determine the nature of roots of the following




Solved Multiplyi 3 5 By 2 5ii 6 15 By 4 3iii 2 6 By 3 3iv3 8 B Self Study 365




Multiplying And Dividing Radical Expressions
RD Sharma Solutions for Class 9 Maths Chapter 3 – Free PDF Download RD Sharma Solutions for Class 9 Maths Chapter 3 – Rationalisation is one of the most important chapters in Class 9RD Sharma Solutions for Class 9 Chapter 3 is about different algebraic identities and rationalisation of the denominatorA rationalisation is a process by which radicals in the denominator of a fractionClick here👆to get an answer to your question ️ Simplify 2√(5)√(3) 1√(3)√(2) 3√(5)√(2)The problem, math (√2√3)^2/math math=(√2)^2(√3)^22(√2*√3)/math math=232√6/math math=52√6/math Now, math 2√6=√24=4
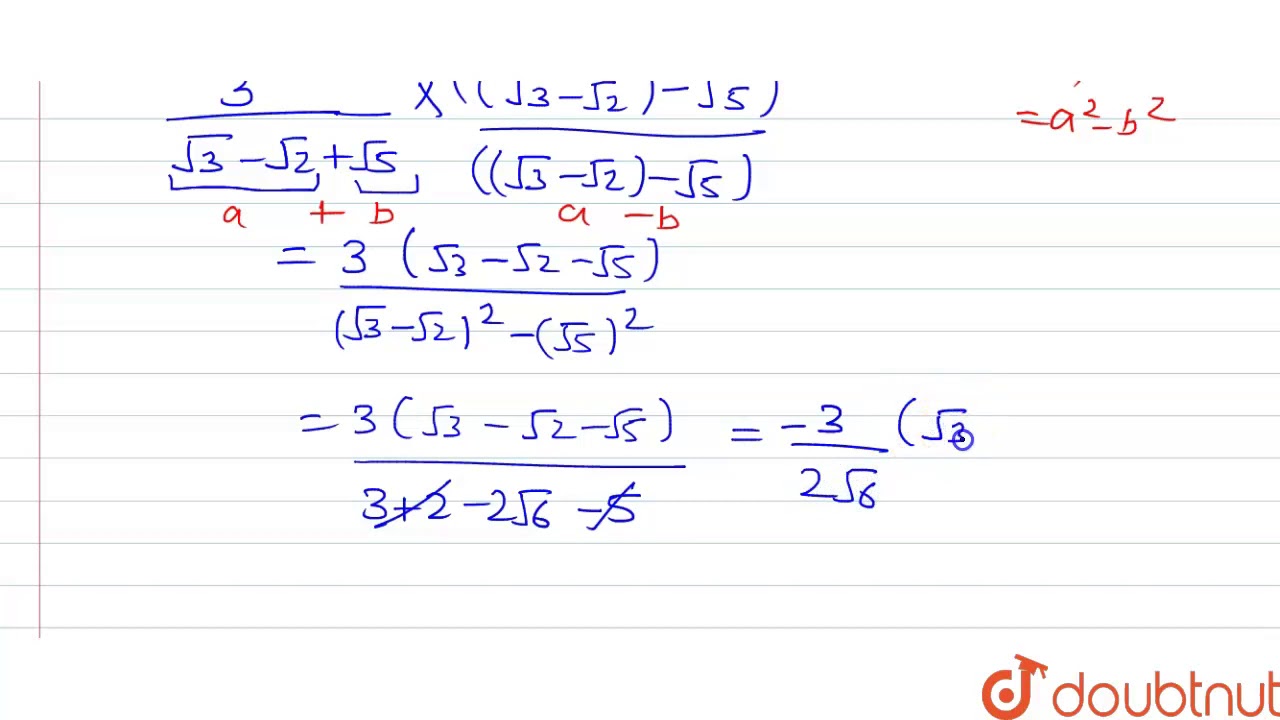



Express 3 Sqrt 3 Sqrt 2 Sqrt 5 With Rational Denominator Youtube




Multiplying And Dividing Radical Expressions
The Solution Set Of Equation 5 2 Root 6 X 2 3 5 2 Root 6 X 2 3 10 Is The solution set of equation (5 2√6) x^23 (5 2√6) x^23 = 10 is 1) {± 2, ± √2}Simplifying this we get 2√3 (3 5 2√5) = 2√3 (2–2√5) = 4√3 4√15 Now both √3 and √15 are irrational We know that rational * irrational is irrational so 4√3 and 4√15 are irrational And also irrational irrational is irrational Therefore 4√3 4√15 is irrational 8 viewsThe square root of 2, often known as root 2, radical 2, or Pythagoras' constant, and written as √ 2, is the positive algebraic number that, when multiplied by itself, gives the number 2It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property Geometrically the square root of 2 is the length of a diagonal across a square




Adding Square Roots Study Com



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline
prove that (32√2)^2n1 (32√2)^2n1 2 is a perfect integral square for every positive integer n3√2 133 2√3 18 What is the distance between z1 = 5 – 2i and z2 = 8 i?We take (2√3) = a equation (2√3) = b equation In a equation we take 2 and Multiply by equation b * (2)×(2√3) Then we multiply 2 by 2 and then 2 by √3 " in above equation" * 2×2 = 4 * 2×√3 = 2√3 Then we add the above equation




Cp Alg 2 5 6 Radical Expressions




Chapter 8 Surds Fraction Mathematics Arithmetic
It is given that 5 − 3 5 3 = a b 1 5 Simplify the term on the LHS by rationalizing, 5 − 3 5 3 × 5 3 5 3 Put on the numeric axis √2; If √x √y = 5, then dy/dx at (4,9) is (a) 2/3 (b) 3/2 (c) 3/2 (d) 2/3 asked in Mathematics by KumariMuskan ( 339k points) bseb model set




E Square Root Of 9 10 2 2 1 2 1 2 3 F Gauthmath




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Updated For 21 22
( (Type an exact answer using radicals as needed use a comma to seSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more What is the distance between z1 = 5 – 2i and z2 = 8 i?




Add 2 3 5 2 And 3 2 2 Brainly In




Vesica Piscis With Square Root Of 2 3 5 The Configuratio Flickr
Evaluate (5/2)^2 ( −5 2)2 ( 5 2) 2 Move the negative in front of the fraction (−5 2)2 ( 5 2) 2 Use the power rule (ab)n = anbn ( a b) n = a n b n to distribute the exponent Tap for more steps Apply the product rule to − 5 2 5 2 ( − 1) 2 ( 5 2) 2 ( 1) 2 ( 5 2) 2 Apply the product rule to 5 2 5 2Solution for Calculează √2 √2 √5 Q 'm thinking of three numbers The product of two of them is 24, and the sum of all three is also 24 Transcript Add (3√27√3) and (√2−5√3) (3√27√3) (√2−5√3) = (3√2√2) (7√3 −5√3) = 𝟒√𝟐 𝟐√𝟑




Add 3 2 7 3 And 2 5 3 Brainly In




5 2 3 7 4 3 A B 3 Find The Value Of A And B Of The Following Brainly In
( (Type an exact answer using radicals as needed use a comma to se answers separate as needed Show all work and Steps ;Rationalise the denominator in each of the following and hence evaluate by taking √2 = 1414, √3 = 1732 and √5 = 2236 up to three places of decimalThe value of 27a 3 – 2√2b 3 is equal to Please scroll down to see the correct answer and solution guide




How To Multiply Square Roots 8 Steps With Pictures Wikihow




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation
Now we will discuss how to prove √2, √3 & √5 is an irrational number Prove that √2 is an irrational number First, Let √2 is a rational number So we may write it as below √2 = a/b Let, where a & b are coprime numbers, means common factor between a & b is 1 b√2 = aGet an answer for 'Simplify 2√27 5√8 3√18 4√12 and show how to do it, please' and find homework help for other Math questions at eNotesSimplify 1/2√3 2/√5√3 1/2√5 Maths NCERT Solutions;




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V



Square Root Of 2 Wikipedia
Hence 2 √5 is an irrational number ii) (3 √23) √23 By simplifying the given expression we get 3 3 = 3/1, which is in the form of p/q and hence a rational number Thus, (3 √23) √23 is a rational number iii) 2√7 / 7√7 2√7 ÷ 7√7 = 2/7, which is in the form of p/q and hence a rational number Thus, 2√7 / 7√7 is Aplicamos diferencia de cuadrados Ésta es su fórmula general ( ab)(ab)=a^2 b^2 Resolvemos (√2√3)(√2√3) (√2)^2 (√3)^2Se van las raíces y potencias y quedaría Find a and b , if 2√5√3/2√5 √3 2√5 √3/2√5√3 = a√15 b Maths Number Systems




Square Root 1 To 10 Value Of Square Roots From 1 To 10 Pdf




Add 2 3 5 5 7 7 And 3 5 3 7 Brainly In
There are 8 sections of seats in an auditoriumQ12 A invests Rs for 2 years at 11% per annum on simple interest and B invests the same money, for the same time and at 10% per annum on compound interest then find the difference between both the interests1 2sqrt(2)1/ 2sqrt2 First multiply bu sqrt(2) ==> 2sqrt(2)*sqrt2 1*sqrt2/2sqrt2*sqrt2 ==> (2*2 sqrt2)/2*2 ==> (4sqrt2)/4 ==> 1sqrt2/4 2 3sqrt2 2sqrt3



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline



Practice Problems On Rationalizing Denominator
Math Secondary School answer answered Add 2√2 5√3 and√2 3√3 2 See answers report flag outlined Both your results are correct and identical in meaning There are many ways to show the answer For example, − √2 √5 2 ∗ √3 √7 2 − 2 5 2 ∗ 3 7 2 So you are really asking a question about what is conventional in presentation The seemingly childish answer to that question is that you should do whatever your teacher A 3√3 5√3 7√3 3√3= 10√38√3= 2√3 b 3√2 43√3 7√2 3√3= 3√2 12√3 7√2 3√3=3√322√3= 19√3




Simplify 4 5 6 2 3 8 3 7 12



Q Tbn And9gcr537uzeasjcwhqukaira 8xguztuift1qdkpgervdfy2mher Usqp Cau
2sinxcosx = 1 − t2 Back to equation (1), we get 2(1 −t2) − 2√3(sinx −cosx) −3 = 0 2 − 2t2 − 2√3t −3 = 0 By changing side, we get a quadratic equation in t 2t2 2sqr3t 1 = 0 (2) D = d2 = b2 − 4ac = 12 −8 = 4 > d = ± 2 The 2 real roots are t = − √3 2 ± 1 2 = −√3 ± 1 2 Jawab d 15 cm² Penjelasan dengan langkahlangkah luas belah ketupat = 1/2 x d1 x d2 = 1/2 x 3√5 x 2√5How to prove 32√5 is an Irrational number



Simplifying By Rationalising The Denominator 3 5 3 2 5 3 Studyrankersonline




Intro To Rationalizing The Denominator Algebra Video Khan Academy
Given x = 3 2√2 Formula Used (a b)2 = a2 2ab b2 Calculation x = 3 2√2 1/x = 1/(3 2√2) ⇒ (3 –& Start Learning Quantitative Aptitude ≫ Algebra ≫ Identities Question (View in Hindi) If x = 3 2√2, then find the value of (√x 1/√x)⇒ (ab) 6 (ab) 6 = 2(6)a 5 b ()a 3 b 3 (6)ab 5 Putting the value of a = √3 and b = √2 in the above equation (√3 √2) 6 (√3 √2) 6Question 1) Find all real solutions √x2 √x3=5 What is the solution set?




4 4 More On Algebra Of Radicals




Find The Square Root Of 5 2 6 M Cube Mathematics By Maheshwari




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




How To Solve 1 1 2 2 3 Quora




Q5 For Each Of The Following N Lido




Surds What Is A Surd Manipulating And Simplifying Surds Ppt Download



What Is The Square Root Of 5 2 Root 6 Quora




Cp Alg 2 5 6 Radical Expressions




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download



2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Ssl Com Wp Content Uploads 15 12 Number H Surds V2 Solutions 1 Pdf




Simplifying The Square Root Of 50 Video Lesson Transcript Study Com



Www Mathsgenie Co Uk Resources 7 Surdsans Pdf




Solved Find Rational Numbers A And B Such That I 2 1 2 1 A B Self Study 365




Rationalize 2 3 5 2 2 3 3 Brainly In




Solve 3 5 3 2 5 A 5 B Youtube



Article 25 Number The Dyad Part 8 Square Roots 2 3 5 Cosmic Core




Given That Root 2 Is Irrational Prove That 5 3 Root3 Is A Scholr




Question Video Finding The Average Rate Of Change Of Root Functions Between Two Points Nagwa



3 2 Square Root Of 5 Square Root Of 62 Square Gauthmath




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




12 Simplify Square Root 32x 5 Y 2 2x 3 Y 3 13 Chegg Com




Add 2 Root 2 5 Root 3 And Root 2 3 Root 3 Youtube



Prove That 3 2 5 Is Irrational Quora




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Updated For 21 22




Add 3 2 7 3 And 2 5 3 Rational Numbers Video Teachoo



Adding Subtracting Radicals Square Roots Purplemath
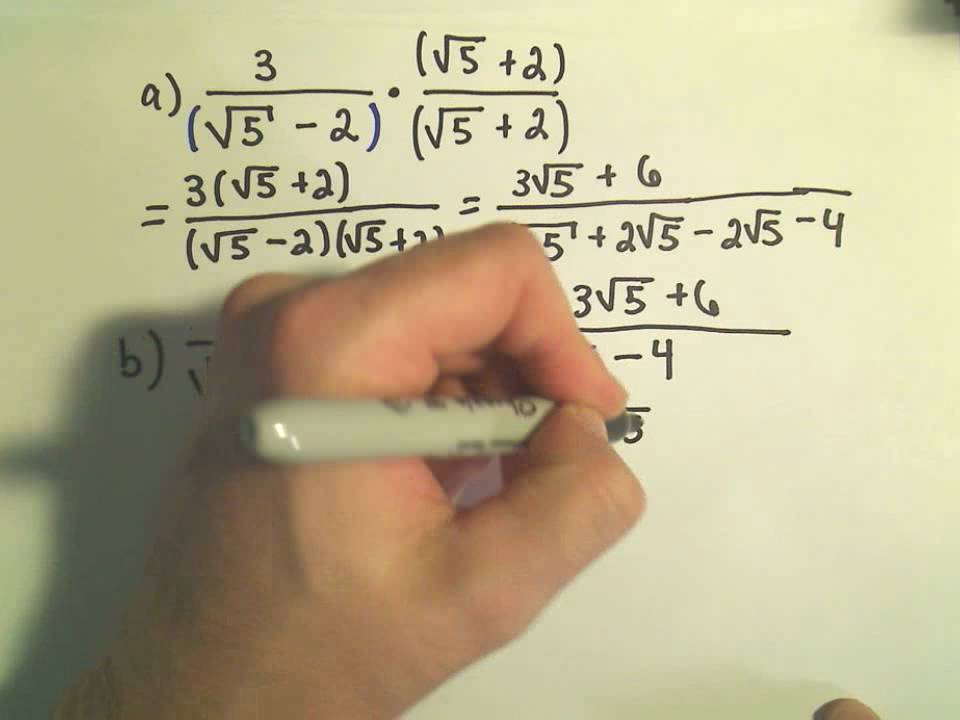



Rationalizing The Denominator Example 1 Youtube




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




Simplifying Square Root Expressions Video Khan Academy
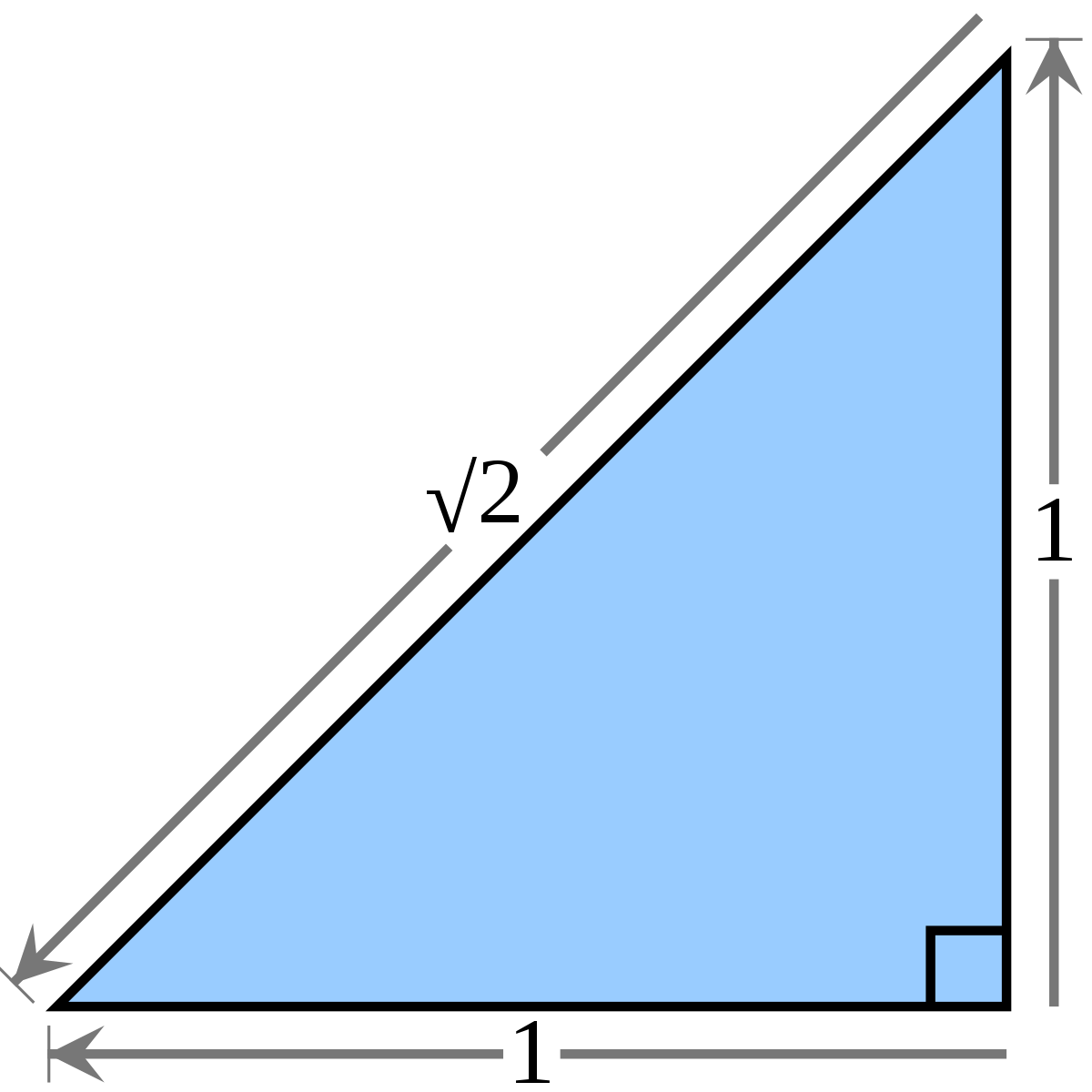



Square Root Of 2 Wikipedia
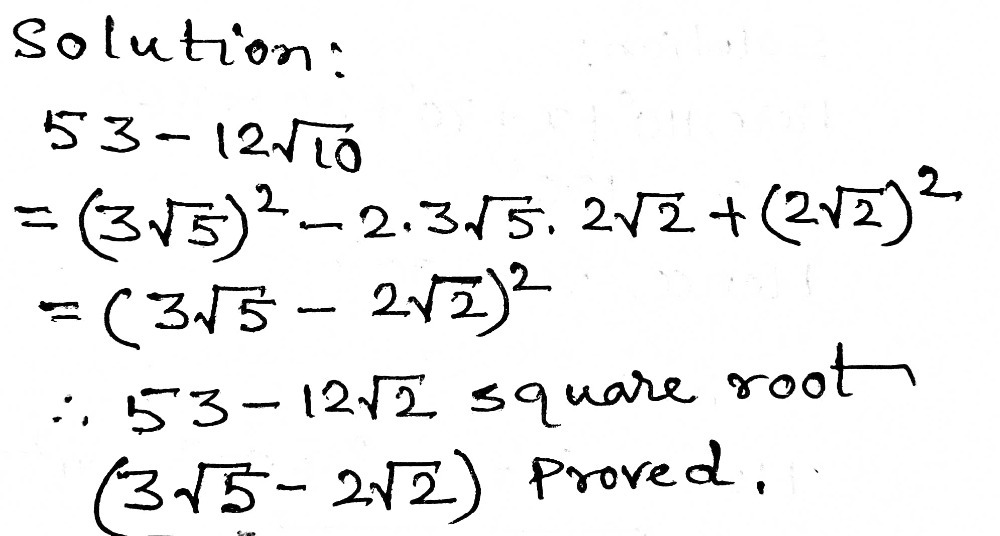



I Show That 3 Square Root Of 5 2 Square Root Of Gauthmath




How To Add And Subtract Square Roots 9 Steps With Pictures




Simplify 2 5 3 1 3 2 3 5 2



Rationalize The Denominator I 1 5 Ii 2 3 7 Iii 1 3 2 Iv 1 3 5 2 2 V 12 4 3 2 Sarthaks Econnect Largest Online Education Community




How To Rationalize Math Frac 1 Sqrt 2 Sqrt 3 Sqrt 5 Math Quora




Telangana Scert Class 9 Math Solution Chapter 1 Real Numbers Exercise 1 4



Plos One Heart Rate Variability In Type 2 Diabetes Mellitus A Systematic Review And Meta Analysis




Rationalise The Denominator Of 2 Sqrt 3 Sqrt 5 Youtube



Express Each One Of The Following With Rational Denominator I 1 3 2 Ii 1 6 5 Iii 16 41 5 Sarthaks Econnect Largest Online Education Community




Multiplying And Dividing Radical Expressions



How To Rationalise The Denominator 1 2 3 5 Quora




Solve 1 Radic 3 Radic 5 Radic 7 Mathematics Topperlearning Com Lwsxcatt
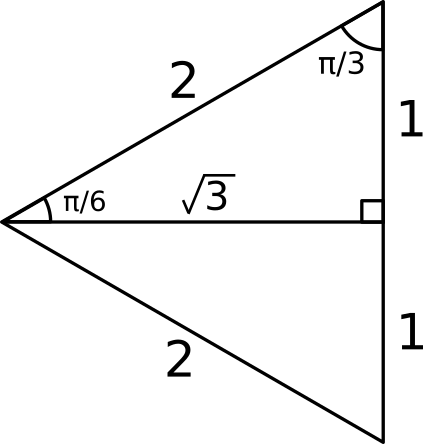



What Is The Square Root Of 3 Divided By 2 Socratic




Square Root 5 Square Root 3 Square Root 15 3 Square Chegg Com




Vesica Piscis Square Root 2 3 5 7 Geometria Sagrada Geometria Materiales Didacticos



What Is The Square Root Of 5 2 Root 6 Quora



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V



Addition And Subtraction Of Surds Assignment Point
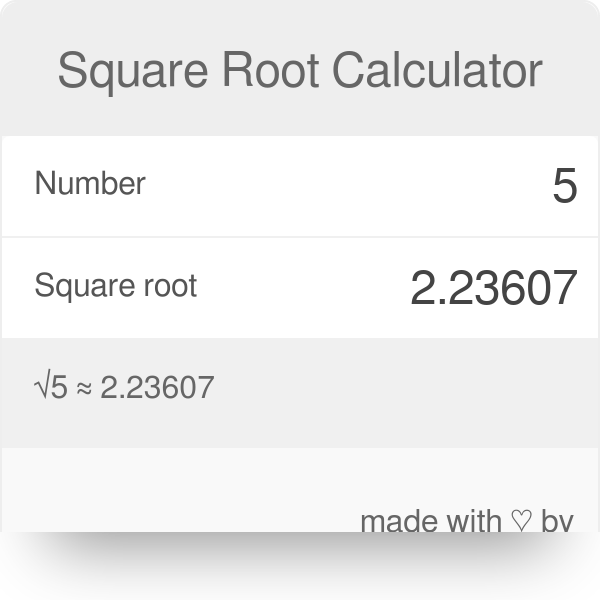



Square Root Calculator Find The Square Root In One Easy Step




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




R D Sharma Solutions Class 10th Ch 1 Real Numbers Exercise 1 5
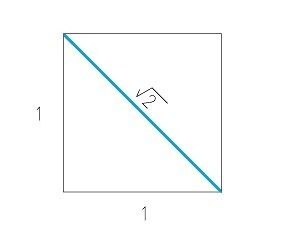



Article 25 Number The Dyad Part 8 Square Roots 2 3 5 Cosmic Core
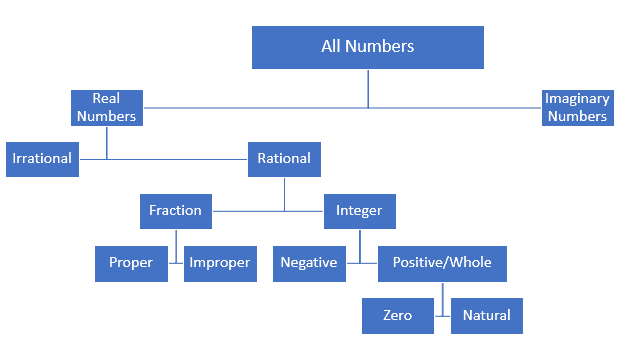



Types Of Numbers Difference And Classification
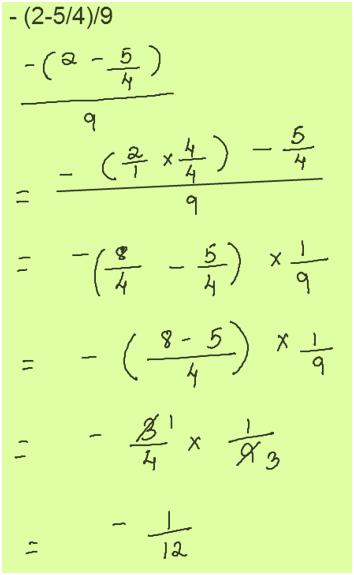



Free Math Answers Answers Within 24 Hours Step By Step Explanations



Square Root Calculator




Surds Objectives Grade A Rationalise The Denominator Of A Surd Such As Grade A Simplify Surds Such As Write In The Form Ppt Download



What Is The Value Of A And B If 5 2 3 7 4 3 A B 3 Quora




Simplifying Square Root Expressions No Variables Video Khan Academy




1 2 Square Roots Of Non Perfect Squares Solutions
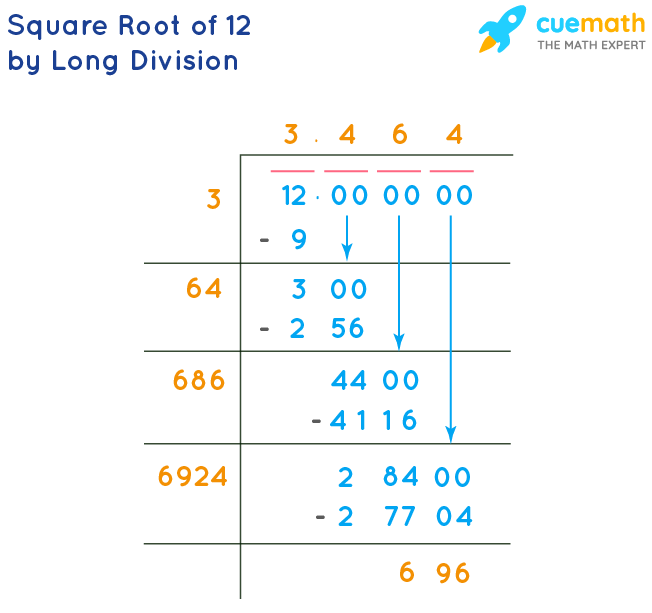



Square Root 1 To 10 Value Of Square Roots From 1 To 10 Pdf
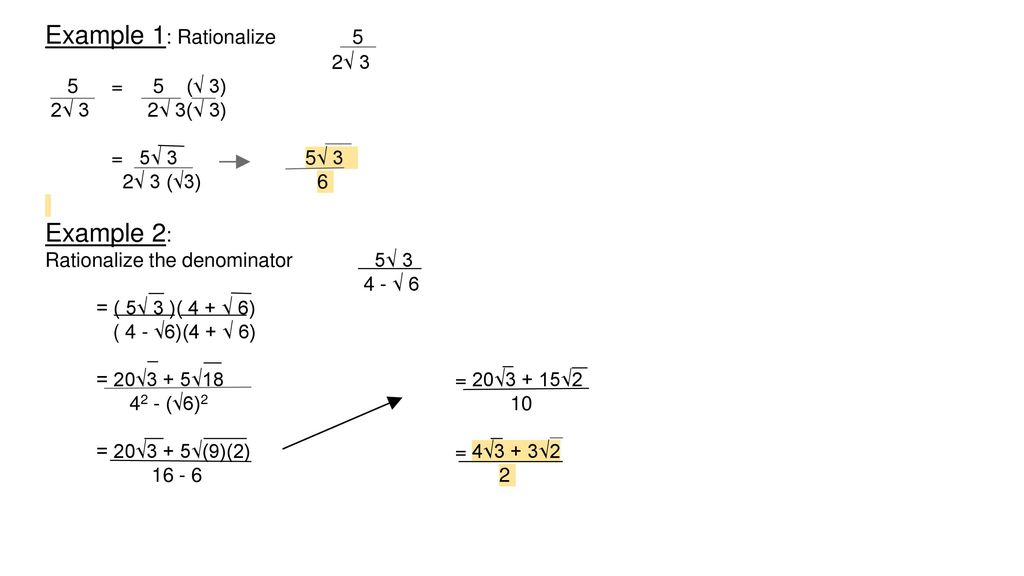



Chapter 5 Radical Expressions And Equations Ppt Download




Wolfram Alpha Examples Step By Step Solutions




Multiplying And Dividing Radical Expressions
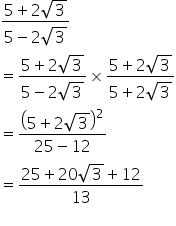



5 2 3 5 2 3 Mathematics Topperlearning Com Rvsvlgmm




4 4 More On Algebra Of Radicals




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is




Square Root Of 2 Wikipedia
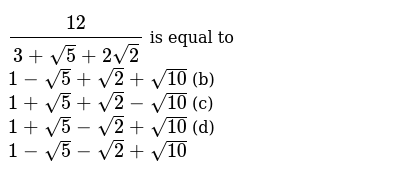



12 3 Sqrt 5 2sqrt 2 Is Equal To 1 Sqrt 5 Sqrt 2 Sqrt 10 B 1 Sqrt 5 Sqrt 2 Sqrt 10 C 1 Sqrt 5 Sqrt 2 Sqrt 10 D 1 Sqrt 5 Sqrt 2 Sqrt 10
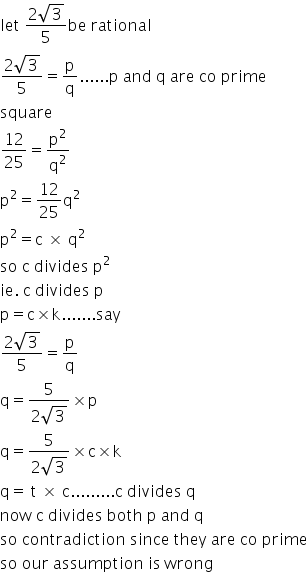



Prove That 2 Root 3 Divided By 5 Is Irrational Mathematics Topperlearning Com Zef8p866




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube



1




Add 2 3 5 2 And 3 2 2 2 2 5 3 7 5 And 3 3 2 5 2 3 7 1 2 2 6 11 Youtube




Mc Ty Surds 09 1



1




How To Add And Subtract Square Roots 9 Steps With Pictures



0 件のコメント:
コメントを投稿